Ensayo Números Reales p4m17

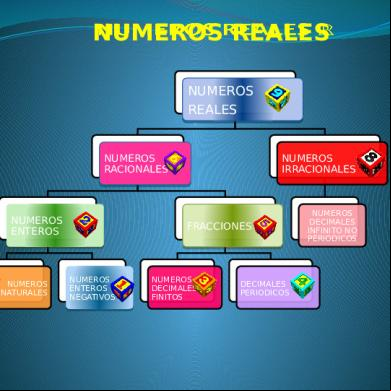
ENSAYO: NÚMEROS REALES Y SUS PROPIEDADES INTRODUCCIÓN: En este trabajo veremos la importancia que tienen los números reales y sus divisiones como son los números enteros, racionales e irracionales, así como también las propiedades de los números reales, que son, Tricotomía, Transitividad, Densidad y Axioma del Supremo. Se puede destacar una propiedad de vital importancia para la Matemática, que es el orden. En otras palabras es un conjunto ordenado (tiene un orden). Esta propiedad se conoce con el nombre de Ley de Tricotomía. La interpretación geométrica de esta propiedad es llamada Transitividad y se define axioma del supremo o axioma de completitud a uno de los axiomas que componen el cuerpo de los números reales. Como rasgo general también es importante señalar que los números reales tienen las siguientes propiedades: de cerradura, conmutativa, asociativa. Existencia del elemento neutro y la existencia del elemento inverso. En un fin trataremos que este desarrollo sirva para la comprensión de dichos números reales y ayude a desarrollar habilidades que necesitaremos en un futuro. DESARROLLO: Los números reales (R) se clasifican en racionales (Q) e irracionales (H). El conjunto de los números reales es de mucha importancia ya que nos ayuda a realizar operaciones pero es indispensable su plena identificación. La estructura de los números reales es: Números enteros. Números naturales (N): cuando contamos los elementos de un conjunto [1,2,3,4,5,6,7,8,9,10,11,12,13,….], comúnmente nos servimos de palabras que pronunciamos, o símbolos que escribimos, en una sucesión ordenada. El conjunto de números naturales no tiene fin, porque siempre será posible agregarle un nuevo elemento; por ello podemos afirmar que se trata de un conjunto infinito los números naturales es también conocido como enteros positivo porque siempre va por la derecha. CÁLCULO DIFERENCIAL PROFESOR: MC. Pérez Limón José Agustín ALUMNA: Mendoza Ochoa Khriemberly Romana

Enteros negativos: ante la dificultad de poder resolver operaciones como 6- 8=, y como en el campo de los números naturales no existe ningún número que sumado a 8 de por resultado 6, surgen los números enteros negativos. Van por la izquierda. Números racionales: Fracciones comunes: se producen cuando deseamos expresar la medida de cantidades que no contienen un número exacto de veces a la unidad elegida o de cantidades menores que dicha unidad. Números irracionales: Los números irracionales también pueden ser positivos y negativos a la derecha del cero se localizarán los irracionales positivos, por lo tanto a la izquierda estarán los negativos. Por ejemplo √2 y √3/2 Propiedad de la Tricotomía ó Ley de Tricotomía: En particular, en los Números Reales, además de las propiedades de producto y suma (que en este conjunto son cerradas), se puede destacar una propiedad de vital importancia para la Matemática, que es el orden. En otras palabras es un conjunto ordenado (tiene un orden). Es decir, si y pertenecen a, entonces se puede decir si la afirmación es verdadera o no.. Nótese que una consecuencia inmediata de esta ley, es que si, entonces es distinto de. Dicho de otra forma, no existe ningún número real tal que. Si imagináramos que es una recta, donde a la izquierda están los números negativos, al "medio" el cero y a la derecha los positivos, entonces, una interpretación geométrica de la afirmación, es que está a la izquierda de. Esta propiedad se cumple en los reales. Esto es porque en general puede representar la cardinalidad de conjuntos (con números), siendo uno de menor o igual cardinalidad que otro. Una relación tricótoma no es simétrica, no es reflexivo, sino es transitiva. Por ejemplo, 3<4, 4<5 ⇒ 3<5. Propiedad Transitiva: Una relación binaria R sobre un conjunto A es transitiva cuando se cumple: siempre que un elemento se relaciona con otro y éste último con un tercero, entonces el primero se relaciona con el tercero. Se conoce como transitividad. En general las relaciones de orden (ser menor, mayor, igual, menor o igual, mayor CÁLCULO DIFERENCIAL PROFESOR: MC. Pérez Limón José Agustín ALUMNA: Mendoza Ochoa Khriemberly Romana

o igual) son transitivas. Tomando el conjunto de los números naturales, y la relación divide a: dado que 3/12 (3 divide a 12) y 12/48 (12 divide a 48), la transitividad establece que 3/48 (3 divide a 48). Sin embargo, no todas las relaciones binarias son transitivas. La relación "no es subconjunto" no es transitiva. Por ejemplo, si X = {1,2,3}, Y={2,3,4,5}, Z={1,2,3,4}. Entonces se cumple Y pero no se cumple puesto que X es subconjunto de Z. Otro ejemplo de relación binaria que no es transitiva es "ser la mitad de": 5 es la mitad de 10 y 10 es la mitad de 20, pero 5 no es la mitad de 20. Propiedad de Densidad: Entre dos números reales diferente a y b, no importa que tan cercano se encuentren, existe otro número real. Los números racionales y los números irracionales son densos en la recta real, una consecuencias de la prioridad de densidad es que cualquier número irracional puede aproximarse tanto como se quiere por medio de un numero racional con una representación decimal. Tome como ejemplo √2 la sucesión de números racionales 1.4142, 1.41421, 1.414213,… avanza constantemente e inexorablemente hacía √ 2. Avanzando lo suficiente en esta sucesión podemos estar tan cerca de √2. Dados dos números reales diferentes y, su promedio está comprendido entre y. Por lo tanto, entre dos números reales sin importar lo cercano que se encuentren, hay una infinidad de números reales. Esto implica que dado un número real cualquiera no tienen sentido expresiones tales como " el número real siguiente a " o " el número real anterior a". Entre dos números reales diferentes hay un número racional, y por lo tanto hay infinitos números racionales entre ellos. Entre dos números reales diferentes hay un número irracional, y por lo tanto hay infinitos números irracionales entre ellos. Propiedad del axioma del supremo: O también axioma de completitud a uno de los axiomas que componen el cuerpo de los números reales. Si es un conjunto no vacío acotado superiormente en, entonces tiene supremo en. Esto permite definir al cuerpo de los números reales como un espacio completo, mientras que, otros cuerpos, como el cuerpo de los números racionales, no lo es. Se dice que un cuerpo ordenado verifica el axioma CÁLCULO DIFERENCIAL PROFESOR: MC. Pérez Limón José Agustín ALUMNA: Mendoza Ochoa Khriemberly Romana

del supremo, cuando todo subconjunto A no vacío de K y acotado tiene supremo en K. Sea A un conjunto de K no vacío y acotado superiormente y sea s una cota superior de A. Como K es arquimediano, existe un elemento natural j ∈ K tal que s < y y j es pues cota superior de A. Sea a ∈ A (existe por ser A no vacío) y elijamos que un entero i ∈ K tal que i < a (si a>0, basta tomar i = 0 y si a -a y basta tomar i = - k). Entonces entre i y j hay elementos de A y ningún elemento de A es mayor de j. Para cada natural n, el conjunto de racionales de denominador n comprendidos entre: i=i.n y j= j.n (todo sobre “n”). Es finito y, por tanto, hay uno mínimo que es cota superior de A. Sea tal elemento m+1 y supongamos a=mn/n CONCLUSIÓN: En mi punto de vista, rescato que los números reales son tan prefectos que es indispensable conocer su conformación para poder resolver algún problema de la vida. Las propiedades de los números reales son: Tricotomía, Transitiva, Densidad y Axioma del Supremo. El primero se destaca una propiedad vital para las Matemáticas, la cual es el orden. Para mayor entendimiento “R” es un conjunto ordenado, es decir, si “x” y “y” pertenecen a “R”, consiste en: -Que si un numero es mayor que otro, no puede ser igual o menor que él. -Si un numero es igual que otro, no puede ser mayor o menor que él. -Si un numero es menor que otro, no puede ser igual o mayor que él. Sobre Transitiva es toda aquella relación binaria “R” sobre un conjunto “A” cuando se cumple siempre que un elemento se relaciona con otro y este a su vez, con un tercero, entonces el primero se relaciona con el tercero. Axioma del Supremo son los axiomas que componen el cuerpo de los números reales, para una explicación más sencilla es: “Si E C R es un conjunto no vacio acotado superiormente en R, entonces E tiene supremo en R”.

CÁLCULO DIFERENCIAL PROFESOR: MC. Pérez Limón José Agustín ALUMNA: Mendoza Ochoa Khriemberly Romana

Culmino que el estudio, pero principalmente el cálculo necesita que yo como estudiante adquiera habilidades y conocimientos totalmente satisfactorios para que un futuro logre crear cosas innovadoras para el bien de la sociedad. FUENTES:  Algebra intermedia, Larson Hosteller Neptune, 2001. Algebra intermedia, Allen R. Ángel, 2008. http://www.monografias.com/trabajos94/numerosreales/numerosreales.shtml#bibli ograa#ixzz2coQV00Be

 http://www.buenastareas.com  http://personales.unican.es/gonzaleof/Sociales_1/reales.pdf

CÁLCULO DIFERENCIAL PROFESOR: MC. Pérez Limón José Agustín ALUMNA: Mendoza Ochoa Khriemberly Romana