Forma General Del Criterio De Falla 1c4e62

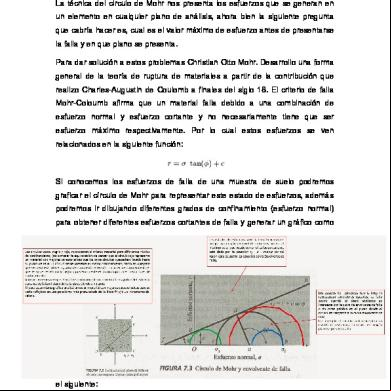
http://www.docfoc.com/140307102-elementos-de-maquinas-hamrock-pdf Pagina para descargar el cengel Forma general del criterio de falla. Un estado multi axial de tensiones en un cuerpo, es el estado más general que puede presentarse ante una condición de solicitación. Componentes ingenieriles pueden estar sujetos a cargas complejas de presión, tracción, compresión, torsión, o una combinación de ellas, de forma tal que para un cierto punto del material se producen tensiones en más de una dirección. En la práctica, suele ser complejo y hasta a veces imposible idear experimentos que puedan cubrir cada detalle y cada particular combinación de tensiones, atento a las dificultades para poder concretarlo como al extraordinario costo que el procedimiento implica. Por tal razón se necesitan Hipótesis, Teorías o Criterios que permitan evaluar, comparar y relacionar un estado de tensión cualquiera con los resultados experimentales del ensayo típico de tracción, cuyo costo es relativamente bajo. En la materia consideraremos dos posibilidades de falla: a) Falla para materiales Dúctiles. b) Falla para materiales Frágiles. En la aplicación de un criterio de falla para materiales dúctiles, la resistencia del material está dada por su resistencia de fluencia, en cambio para un criterio de falla para materiales frágiles la tensión límite será la tensión de rotura a la tracción. Los criterios de falla para materiales isotrópicos pueden ser expresados en la forma matemática siguiente:

Las teorías de fallas se dividen en dos grupos:

Erick Santiago Morales Huerta

Falla de materiales dúctiles: Un material es dúctil si más del 5% de deformación antes de la fractura. En los materiales dúctiles se considera que la falla se presenta cuando el material empieza afluir o también cuando ocurre la falla por deformación.

Teoría del Esfuerzo Cortante Máximo: También conocida como Teoría de Tresca. Establece que la fluencia del material se produce por el esfuerzo cortante, surgió de la observación de la estricción que se produce en una probeta cuando es sometida a un ensayo de tensión. La teoría dice: “La falla se producirá cuando el esfuerzo cortante máximo absoluto en la pieza sea igual o mayor al esfuerzo cortante máximo absoluto de una probeta sometida a un ensayo de tensión en el momento que se produce la fluencia” Para un elemento bajo la acción de esfuerzos tenemos el círculo de Mohr:

El esfuerzo cortante máximo absoluto es entonces:

Erick Santiago Morales Huerta

El círculo de Mohr para el ensayo de tensión en el momento de la fluencia es:

El esfuerzo cortante máximo absoluto es entonces para el ensayo de tensión al momento de la fluencia:

Según la teoría de Tresca, igualamos las ecuaciones anteriores tenemos:

La ecuación anterior se utiliza cuando

σ 1 >0> σ 3 En los otros casos:

En el plano σ 1−σ 3 , la teoría de Tresca se representa gráficamente como:

Erick Santiago Morales Huerta

La falla se presentará cuando el punto determinado por los esfuerzos σ 1 y σ 3

se

encuentra fuera del área sombreada en la figura 2.3.

Teoría de la Energía de Distorsión: CRITERIO DE FALLA DE LA MAXIMA ENERGIA DE DISTORSION. (También conocido como teoría de Hubert-Mises-Hencky) Este es otro criterio comúnmente empleado para metales dúctiles, y dice que el principio de fluencia se produce cuando la energía de distorsión alcanza un valor crítico. La falla se producirá cuando la energía de distorsión por unidad de volumen debida a los esfuerzos máximos absolutos en el punto crítico sea igual o mayor a la energía de distorsión por unidad de volumen de una probeta en el ensayo de tensión en el momento de producirse la fluencia. Esta teoría se originó de la observación que los materiales dúctiles sometidos a esfuerzos hidrostáticos presentan resistencias a la fluencia que exceden en gran medida los valores que resultan del ensayo de tensión simple, dice que la fluencia no es un fenómeno de tensión o compresión simples, sino que está relacionada con la energía proveniente de la distorsión (angular) del elemento de esfuerzo. Erick Santiago Morales Huerta

Teniendo como ecuación central:

Teoría de Coulomb-Mohr Dúctil También conocida como Teoría de la Fricción Interna (IFT). Ésta teoría tiene encuenta que el esfuerzo de fluencia a tensión (Syt) es diferente al esfuerzo de fluencia acompresión (Syc), donde generalmente Syc > Syt. Se basa en los ensayos de tensión y compresión, y establece que en el plano σ −τ la línea tangente a los círculos de Mohr de los ensayos de tensión y compresión al momento de la fluencia es la locación de la falla para un estado de esfuerzos en un elemento.

La ecuación de la línea de falla cuando σ 1 >0> σ 3

En los otros casos, la falla se dará cuando:

Erick Santiago Morales Huerta

resulta ser:

En el plano σ 1−σ 3 la teoría de Coulomb-Mohr Dúctil se representa gráficamente como:

La falla se presentará cuando el punto determinado por los esfuerzos σ 1 y σ 3

se

encuentra fuera del área sombreada en la figura 2.7. La línea más gruesa representa las locaciones donde se presentará la falla de acuerdo con Coulomb-Mohr, las líneas interiores más delgadas representan las locaciones de falla de acuerdo con Tresca. De la figura 2.7 puede observarse que la teoría de Coulomb-Mohr tiene un mayor área en la cual no se presentará falla que la teoría de Tresca, por eso y por lo que se ha hecho notar de la teoría de la energía de distorsión., es que la teoría del esfuerzo cortante máximo es la teoría escogida para hacer cálculos conservadores de falla de un material y tener mayor certeza de que no se producirá falla.

2. TEORIA DE FALLA POR ENERGÍA DE DEFORMACIÓN MÁXIMA: La falla ocurre en una parte cuando la energía de deformación por volumen unitario exceda la de una prueba de tensión uniaxial en la falla.

Para determinar la energía de deformación por volumen unitario:

Sea el bloque de dimensiones diferenciales de la figura 1, sobre el cual actúan los esfuerzos normales principales: Erick Santiago Morales Huerta

Figura 1. Bloque con esfuerzos unitarios.

La energía de deformación es el trabajo realizado por estas fuerzas al desplazar el cubo una distancia l.

La energía de deformación U es igual al trabajo necesario para deformar el cubo:

U  W   F .l

(1)

Para causar esta deformación, la fuerza causada por cada esfuerzo  es:

Fx final   1d y d z Fy final   2 d x d z Fz final   3 d x d y º (2)

Puesto que el estiramiento depende linealmente de la fuerza aplicada, este comportamiento se puede mostrar como en la gráfica 3.

Erick Santiago Morales Huerta

Figura 2. comportamiento lineal de fuerza por desplazamiento

W Por lo tanto: U deformación 

F .l 2

(3)

FX final.x Fy final.y Fz final   2 2 2

(4)

Además como:

1  2 

l l

3

x

dx y  dy z  dz

x   1 .dx y   2 .dx z   3 .dx

luego

Por la ley de Hooke se tiene que:

1 .  1   2   3  E 1  2  .  2   1   2  E 1  3  .  3   1   3  E

1 

Erick Santiago Morales Huerta

(6)

(5)

Por lo tanto:

 1 dy dz dx  1   2   3    2 dx dz dy  2   1   3    3 dx dy dz  3   1   2  2E 2E 2E dy dz dx 2 2 2 U  1   2   3  2   1 2   1 3   2 3  2E U





(13) Como es por volumen unitario, se divide por dx dy dz:







1  1 2   2 2   3 2  2   1 2   1 3   2 3  2E

(7)

Por razonamiento similar la energía de deformación por volumen unitario en la prueba de tensión es:

 fy 

1 2  yp 2E

(8)

Y finalmente se tiene para diseñar:

2

2

Falla de materiales frágiles

Erick Santiago Morales Huerta

2

  yp 

 1   2   3  2   1 2   1 3   2 3    2



 N  fs  

 para diseñar

(9)

Un material es frágil si tiene menos del 5% de deformación antes de la fractura. En los materiales frágiles se considera que la falla se presenta cuando el material sufre de separación de sus partes (falla por fractura). 1. TEORÍA DE FALLA POR ESFUERZO NORMAL MÁXIMO La falla ocurrirá en la parte di cualquiera de los esfuerzos normales principales excede el esfuerzo normal principal que da lugar a la falla en la prueba uniaxial simple.

Si:

S1 = Esfuerzo Principal 1

yc = Esfuerzo de fluencia a compresión

S2 = Esfuerzo Principal 2

yt = Esfuerzo de fluencia a tensión.

S3 = Esfuerzo Principal 3. Se debe cumplir que:

 yc  S1   yt  yc  S 2   yt  yc  S 3   yt (1)

Si se aplica un factor de diseño se consiguen las ecuaciones de diseño:

 yc nd

 yc nd

 yc nd

 S1   S2   S3 

 yt nd

 yt nd

 yt nd

(2)

Para materiales frágiles yc o yt es el esfuerzo de fluencia.

Erick Santiago Morales Huerta

Teoría de Coulomb-Mohr Frágil Se deriva de forma similar a la teoría de Coulomb-Mohr Dúctil sólo que, al tratarse de materiales frágiles, se tienen en cuenta las resistencias últimas del material a la tensión y compresión en lugar de los esfuerzos de fluencia. La ecuación de la línea de falla cuando σ 1 >0> σ 3

resulta ser:

En los otros casos, la falla se dará cuando:

En el plano σ 1 y σ 3 la teoría de Coulomb-Mohr Frágil se representa gráficamente como:

La falla se presentará cuando el punto determinado por los esfuerzos σ 1 y σ 3 se encuentra fuera del área sombreada en la figura 3.2.

Erick Santiago Morales Huerta